1. In Example 4.1, if $\pi$ is the equiprobable random policy, what is $q_\pi(11, \text{down})$? What is $q_\pi(7, \text{down})$?
Solution:
In the first case, since we are guaranteed to terminate,
$$ \begin{align*} q_\pi(11, \text{down}) &= \sum_{s', r} p(s', r | 11, \text{down})[r + v_\pi(s')] \\ &= (1) \cdot (-1 + 0) = -1 \end{align*} $$
Recall from Problem 3.19, we can express $q_\pi(s, a)$ in terms of $v_\pi(s)$:
$$ q_\pi(s, a) = \sum_{s', r} p(s', r | s, a)[r + v_\pi(s')] $$
Thus,
$$ \begin{align*} q_\pi(7, \text{down}) &= \sum_{s', r} p(s', r | 7, \text{down})[r + v_\pi(s')] \\ &= (1) \cdot (-1 + v_\pi(11)) \\ &= (1) \cdot (-1 + (-14)) = -15 \end{align*} $$
2. In Example 4.1, suppose a new state 15 is added to the gridworld just below state 13, and its actions, $\texttt{left}$, $\texttt{up}$, $\texttt{right}$, and $\texttt{down}$, take the agent to states 12, 13, 14, and 15, respectively. Assume that the transitions from the original states are unchanged. What, then, is $v_\pi(15)$ for the equiprobable random policy? Now suppose the dynamics of state 13 are also changed, such that action $\texttt{down}$ from state 13 takes the agent to the new state 15. What is $v_\pi(15)$ for the equiprobable random policy in this case?
Solution:
In the first case, we have:
$$ \begin{align*} v_\pi(15) &= \sum_a \pi(a|15) \sum_{s', r} p(s', r | 15, a)[r + v_\pi(s')] \\ &= \frac{1}{4} \left[ -1 + v_\pi(12) \right] + \frac{1}{4} \left[ -1 + v_\pi(13) \right] + \frac{1}{4} \left[ -1 + v_\pi(14) \right] + \frac{1}{4} \left[ -1 + v_\pi(15) \right] \\ &= -1 + \frac{1}{4} \left[ v_\pi(12) + v_\pi(13) + v_\pi(14) + v_\pi(15) \right] \\ \Rightarrow v_\pi(15) &= -\frac{4}{3} + \frac{1}{3} \left[v_\pi(12) + v_\pi(13) + v_\pi(14)\right] \\ &= -\frac{4}{3} + \frac{1}{3} \left[ -22 -20 -14 \right] = -\frac{4 + 56}{3}= -20 \end{align*} $$
For the second case, we can "manually" apply policy evaluation, starting from the value function obtained for the first case. Applying to $v_\pi(13)$, we have:
$$ \begin{align*} v_\pi'(13) &= \sum_a \pi(a|13) \sum_{s', r} p(s', r | 13, a)[r + v_\pi(s')] \\ &= \frac{1}{4} \left[ (-1 + v_\pi(9)) + (-1 + v_\pi(12)) + (-1 + v_\pi(14)) + (-1 + v_\pi(15)) \right] \\ &= -1 + \frac{1}{4} \left[ -20 -22 -14 -20 \right] = -1 - 19 = -20. \end{align*} $$
Repeating the calculation for $v_\pi'(15)$ yields the same result as before, so $v_\pi'(15) = -20$. The Bellman equation will be satisfied for all other states at their initial values, so these values are the true values, i.e., $v_\pi'(13) = v_\pi(13) = -20$ and $v_\pi'(15) = v_\pi(15) = -20$.
3. What are the equations analogous to (4.3), (4.4), and (4.5), but for action-value functions instead of state-value functions?
Solution:
$$ \begin{align*} q_\pi(s, a) &= \mathbb{E}_\pi[G_t | S_t = s, A_t = a] \\ &= \mathbb{E}_\pi[R_{t+1} + \gamma G_{t+1} | S_t = s, A_t = a] \\ &= \mathbb{E}_\pi[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) | S_t = s, A_t = a] \tag{cf. 4.3} \\ &= \sum_{s', r} p(s', r | s, a)[r + \gamma \sum_{a'} \pi(a' \mid s') q_\pi(s', a')] \tag{cf. 4.4} \\ \Rightarrow q_{k+1}(s, a) &= \sum_{s', r} p(s', r | s, a)[r + \gamma \sum_{a'} \pi(a' \mid s') q_k(s', a')] \tag{cf. 4.5} \end{align*} $$
4. The policy iteration algorithm on page 80 has a subtle bug in that it may never terminate if the policy continually switches between two or more policies that are equally good. This is okay for pedagogy, but not for actual use. Modify the pseudocode so that convergence is guaranteed.
Solution:
Assume the $\arg\max$ operator returns a set of actions, rather than a single action. Furthermore, assume that $\mathcal{A}$ has a partial order (i.e., given two actions $a_1, a_2 \in \mathcal{A}$, we can determine if $a_1 \leq a_2$). This can be done by encoding the actions as integers, for example.
Then, we can modify the policy iteration algorithm as follows:
$$ \begin{align*} &\textit{policy-stable} \leftarrow \textit{true} \\ &\text{For each } s \in \mathcal{S} \\ &\quad \textit{old-action} \leftarrow \pi(s) \\ &\quad \pi(s) \leftarrow \min \underset{a}{\text{argmax}} \sum_{s', r} p(s', r | s, a)[r + \gamma V(s')] \\ &\quad \text{If } \textit{old-action} \neq \pi(s) \text{, then policy-stable} \leftarrow \textit{false} \\ &\text{If } \textit{policy-stable} \text{, then stop and return } V \approx v_*, \pi \approx \pi_* \text{; else go to 2}\\ \end{align*} $$
This modification "breaks ties" in the policy selection process by choosing the "minimum" action.
5. How would policy iteration be defined for action values? Give a complete algorithm for computing $q_*$, analogous to that on page 80 for computing $v_*$. Please pay special attention to this exercise, because the ideas involved will be used throughout the rest of the book.
Solution:
Initialization $$Q(s, a) \in \mathbb{R} \text{ and } \pi(s) \in \mathcal{A} \text{ for all } s \in \mathcal{S} \text{ and } a \in \mathcal{A}(s); Q(\textit{terminal}, a) = 0$$
Policy Evaluation
$$ \begin{align*} \text{Loop:} \\ &\Delta \leftarrow 0 \\ &\text{Loop for each } s \in \mathcal{S}: \\ &\quad \text{Loop for each } a \in \mathcal{A}(s): \\ &\quad \quad q \leftarrow Q(s, a) \\ &\quad \quad Q(s, a) \leftarrow \sum_{s', r} p(s', r | s, a)[r + \gamma \sum_{a'} \pi(a' | s') Q(s', a')] \\ &\quad \quad \Delta \leftarrow \max(\Delta, |q - Q(s, a)|) \\ &\text{Until } \Delta < \theta \text{ (a small positive number determining the accuracy of the estimation)} \end{align*} $$
Policy Improvement $$ \begin{align*} &\text{policy-stable} \leftarrow \text{true} \\ &\text{For each } s \in \mathcal{S}: \\ &\quad \text{old-action} \leftarrow \pi(s) \\ &\quad \pi(s) \leftarrow \min \underset{a}{\text{argmax}} Q(s, a) \\ &\quad \text{If } \text{old-action} \neq \pi(s) \text{, then policy-stable} \leftarrow \text{false} \\ &\text{If } \text{policy-stable}, \text{then stop and return } Q \approx q_* \text{ and } \pi \approx \pi_* \text{; else go to 2} \end{align*} $$
6. Suppose you are restricted to considering only policies that are $\epsilon$-soft, meaning that the probability of selecting each action in each state, $s$, is at least $\epsilon/|\mathcal{A}(s)|$. Describe qualitatively the changes that would be required in each of the steps 3, 2, and 1, in that order, of the policy iteration algorithm for $v_*$ on page 80.
Solution:
In step 3, we would need to ensure the resulting policy is $\epsilon$-soft. This could be done by, after checking for stability, converting the policy to be $\epsilon$-greedy, i.e., with probability $1 - \epsilon$, select the action that maximizes the (current estimate of the) value function, and with probability $\epsilon$, select an action at random.
Then, in step 2, we would need to ensure that the policy evaluation step is consistent with the $\epsilon$-soft policy. This would be done by modifying the the Bellman update:
$$V(s) \leftarrow \sum_a \pi(a|s) \sum_{s', r} p(s', r | s, a)[r + \gamma V(s')].$$
Finally, in step 1, we would need to ensure that the initialization of the policy is $\epsilon$-soft. After arbitrarily choosing the "main" action for each state, set the probability of selecting any other action to be at least $\epsilon/|\mathcal{A}(s)|$.
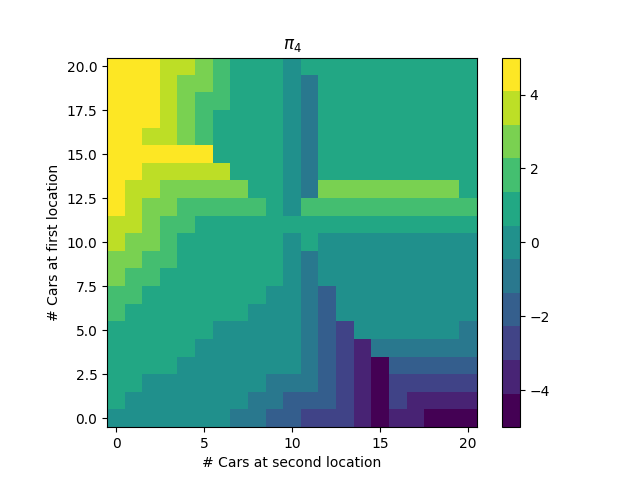
7. (Programming) Write a program for policy iteration and re-solve Jack's car rental problem with the following changes. One of Jack's employees at the first location rides a bus home each night and lives near the second location. She is happy to shuttle one car to the second location for free. Each additional car still costs 2 dollars, as do all cars moved in the other direction. In addition, Jack has limited parking space at each location. If more than 10 cars are kept overnight at a location (after any moving of cars), then an additional cost of 4 dollars must be incurred to use a second parking lot (independent of how many cars are kept there). These sorts of nonlinearities and arbitrary dynamics often occur in real problems and cannot easily be handled by optimization methods other than dynamic programming. To check your program, first replicate the results given for the original problem.
Solution:
The optimal policy:
8. Why does the optimal policy for the gambler's problem have such a curious form? In particular, for capital of 50, it bets it all on one flip, but for capital of 51 it does not. Why is this a good policy?
Solution:
If the gambler has a capital of 50, they have a 50% chance of winning the game by betting it all. If they have a capital of 51, and bet $1, they either end up with 50 or 52. Thus, following this policy means they have a 50% chance of getting the same "do-or-die" situation at a capital of 50, and a 50% chance of making progress towards the "safer" state of 75, where they can bet it all without risk of losing the game.
9. (Programming) Implement value iteration for the gambler's problem and solve it for $p_h = 0.25$ and $p_h = 0.55$. In programming, you may find it convenient to introduce two dummy states corresponding to termination with capital of 0 and 100, giving them values of 0 and 1, respectively. Show your results graphically, as in Figure 4.3. Are your results stable as $\theta \rightarrow 0$?
Solution:
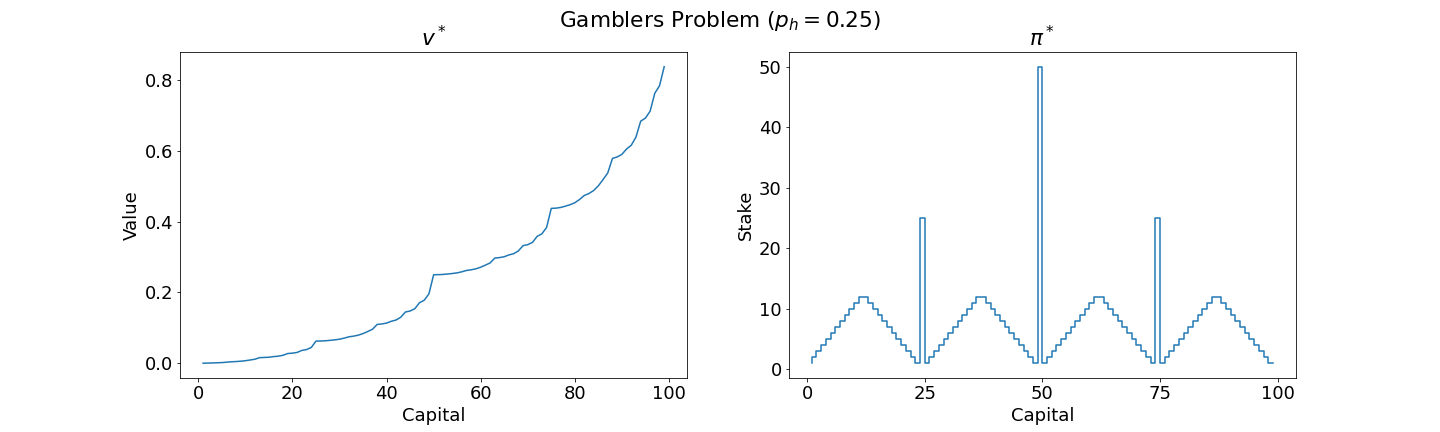

Results are stable as $\theta \rightarrow 0$.
10. What is the analog of the value iteration update (4.10) for action values, $q_{k+1}(s, a)$?
Solution:
The update is:
$$q_{k+1}(s, a) = \sum_{s', r} p(s', r | s, a)\left[ r + \gamma \max_{a'} q_k(s', a') \right].$$
The complete algorithm is:
$$ \begin{align*} &\text{Initialize $Q(s,a)$, for all $s \in \mathcal{S}^+$, $a \in \mathcal{A}(s)$, arbitrarily except that $Q($terminal$, a) = 0$} \\ &\text{Loop} \\ &\quad \Delta \leftarrow 0 \\ &\quad \text{Loop for each $s \in \mathcal{S}$}: \\ &\quad \quad \text{Loop for each $a \in \mathcal{A}(s)$} \\ &\quad \quad \quad a \leftarrow Q(s, a) \\ &\quad \quad \quad Q(s, a) \leftarrow \sum_{s', r} p(s', r | s, a)\left[ r + \gamma \max_{a'} Q(s', a') \right] \\ &\quad \quad \quad \Delta \leftarrow \max(\Delta, |q - Q(s, a)|) \\ &\text{until } \Delta < \theta \\ \\ &\text{Output a deterministic policy, $\pi \approx \pi_*$, such that}\\ & \pi(s) = \arg\max_a Q(s, a) \end{align*} $$