Duolingo Leagues

Duolingo pools users into ten leagues (from Bronze, Silver, …, Diamond). Each week, the top XP-scoring members of each league are promoted and the bottom scoring-XP members are demoted (the specifics are here). Assuming no users enter, this can be modeled as a discrete time Markov chain:

\[\mathbf{x}_{n+1} = \mathbf{A}\mathbf{x}_n\]

where $\mathbf{x}_i$ is the vector of population levels for each league in week $i$ and $\mathbf{A}$ is a tridiagonal, irreducible, left-stochastic matrix representing the transitions. Starting from a distribution where everyone is in the bottom three leagues, and assuming no one enters or leaves, we observe the existing transition rules push populations towards the higher leagues:

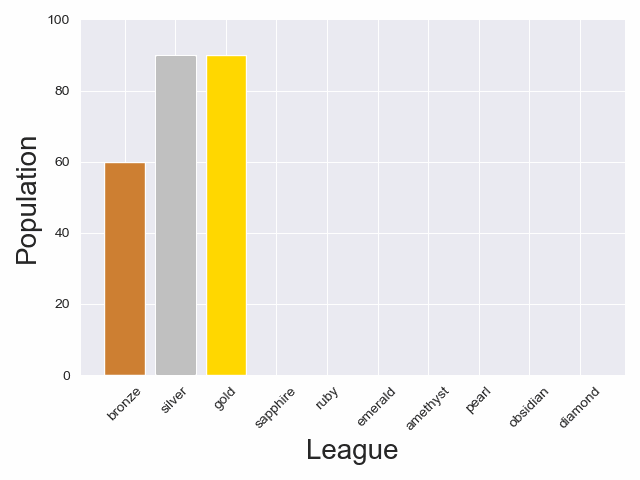
We can calculate this steady state distribution using linear algebra. In particular, we identify the principal eigenvector of $\mathbf{A}$, which will be associated with an eigenvalue of 1.

A question I have: Can one construct a triadiagonal, irreducible left-stochastic matrix $\mathbf{A}$, given a specified principal eigenvector? This would be of use to Duolingo, if say, they wanted most users to be near the top (i.e., in the pearl and obsidian leagues).

One idea is to cast this as a constraint satisfaction problem. In particular, we can create the following formulation, where the decision variables, $a_{ij}$, are the entries of the matrix $\mathbf{A}$, $\mathbf{v}$ is the (given) dominant eigenvector, and $\epsilon > 0$ is a given minimum transition proportion:

\[\begin{align} \sum_{j=1}^n a_{ij}v_j &= v_i \quad &\forall i \in \{1,\dots,n\} \\ \sum_{i=1}^n a_{ij} &= 1 \quad &\forall j \in \{1,\dots,n\} \\ a_{ij} &= 0 \quad &\forall i,j \in \{1,\dots,n\}, |i-j| > 1 \\ a_{ij} &\ge \epsilon \quad &\forall i,j \in \{1, \dots, n\}, |i-j| \le 1 \\ 0 \le a_{ij} &\le 1 \quad &\forall i,j \in \{1, \dots, n\} \end{align}\]

Here, constraints (1) assert that $\mathbf{v}$ is an eigenvector of $\mathbf{A}$, with eigenvalue 1. Constraints (2) and (5) ensure that $\mathbf{A}$ is left-stochastic (by enforcing column sums to equal 1, and entries to be between 0 and 1). Constraints (3) limit our search to tridiagonal matrices. Constraints (4) enforce the matrix to be irreducible, by guaranteeing all elements on the tridiagonal are at least $\epsilon > 0$.

Constraints (4) are a little bit of a hack. You don’t need all elements on the tridiagonal to be strictly positive in order to guarantee irreducibility, and so we are cutting off feasible solutions. However, I haven’t yet found a way to express the irreducibility with a linear constraint.

However, with $\epsilon$ set to 0.01, for a given $\mathbf{v}$, CPLEX was able to find a solution. I set a target distribution 5% for the bottom five leagues, 10% for the emerald and amythest, 20% for pearl, 30% for obsidian, and 5% for diamond. The resulting transition matrix then leads a random distribution towards the target. The convergence, however, is rather slow (it takes 3500 weeks to get there):